The sweet spot for tennis Grand Slams
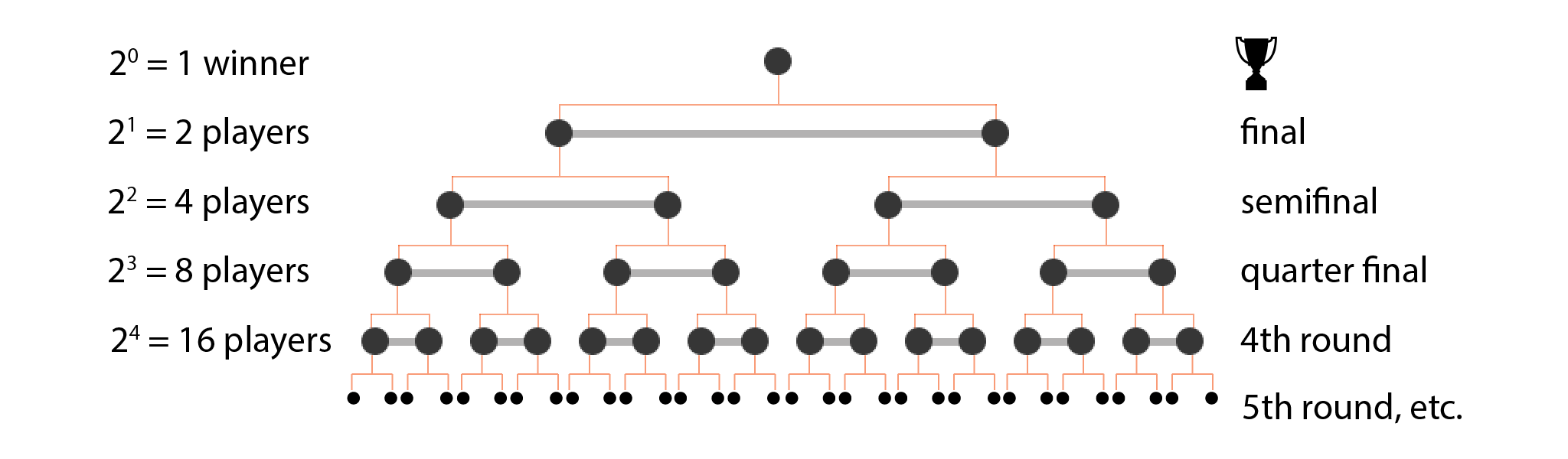
Grand Slams use a single-elimination tournament structure, which means a player is eliminated as soon as they lose a match. To avoid byes (having some players sit out the first round), the number of tournament entrants must be a number you can get by multiplying 2 over and over again. This is known as base 2 to the power of x, and in this case, x is the number of rounds in the tournament. The Australian Open has 7 rounds, so to find the total number of entrants we need to raise 2 to the power of 7 (that is, 2⁷), which equals 128.
2⁷ = 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128
To see this, let’s start at the end—we only have one winner, so the last round involves 1 final match involving 2 (2¹) players—and those 2 players must have won their respective semifinals. So, there must have been 2 semifinal matches played in the previous round, involving 4 players in total—and those 4 players must have won their respective quarter finals.
So, there must have been 4 quarter final matches played in the previous round, with 8 players in total … and the pattern emerges! Since the number of players halves as we progress through the rounds (the winners keep playing, whereas the runners-up are eliminated), the number of players must double as we move backwards from the final to the first round.
All that doubling means that the number of starting players in each round must be 2 (2¹), 4 (2²), 8 (2³), 16 (2⁴), 32 (2⁵), 64 (2⁶), 128 (2⁷), 256 (2⁸) or even larger powers of 2. Grand Slams have 128 players because it’s the ‘Goldilocks’ option—not too few players (as 64 would be), not too many (as 256 would be)—it’s ‘just right’.