The mathematics of voting
Expert reviewers
Essentials
- All voting systems are underpinned by mathematics
- In Australia, a candidate needs a majority of the votes to win a seat (as opposed to the ‘first past the post’ system, where whoever has the greatest number of votes wins)
- There are 150 Members elected to the House of Representatives, from electorates of around 94,000 voters
- To elect the House of Representatives, voters use a ‘preferential system’ to vote for several candidates in their order of preference, rather than just a single candidate. Preferences are allocated until a candidate has a majority of votes
- There are eight Senate electorates—the six states and two Territories. Regardless of their population numbers, each state elects 12 Senators, and each Territory elects two.
- To elect Senators, voters again use a preferential system, but because more than one candidate is elected at a time, a complex equation quota system is used to determine the winning candidates
There are almost as many different voting systems in the world as there are elected assemblies. The one thing they all have in common is their reliance on mathematics to calculate the results.
In Australia, we elect a group of people, a Parliament, to make decisions and laws on behalf of the whole country. We elect a new Parliament approximately every 3 years. At this time each adult citizen votes for the candidates in their electorate who they think will make the best decisions on their behalf. Candidates are then elected according to votes received, in accordance with the Australian electoral system.
While there are many different electoral systems around the world, all are based on mathematical criteria of fairness. However, electoral systems are generally chosen or refined for political rather than mathematical reasons.
The system used in Australia was based partly on the British Westminster system and partly on the American system. Over time some distinctly Australian characteristics have developed, such as the principle of ‘one person, one vote’, and a candidate needing to receive a majority of votes to be elected.
Many countries still use the ‘first past the post’ system, where the candidate with the highest number of votes wins. The problem with this system is that the person with the most votes may still have less than half of all the votes.
For example, let’s say that Anna, Brett, Christine and Daniel are candidates in an electorate where 100 votes are cast as follows: Anna 36, Brett 30, Christine 23, and Daniel 11.
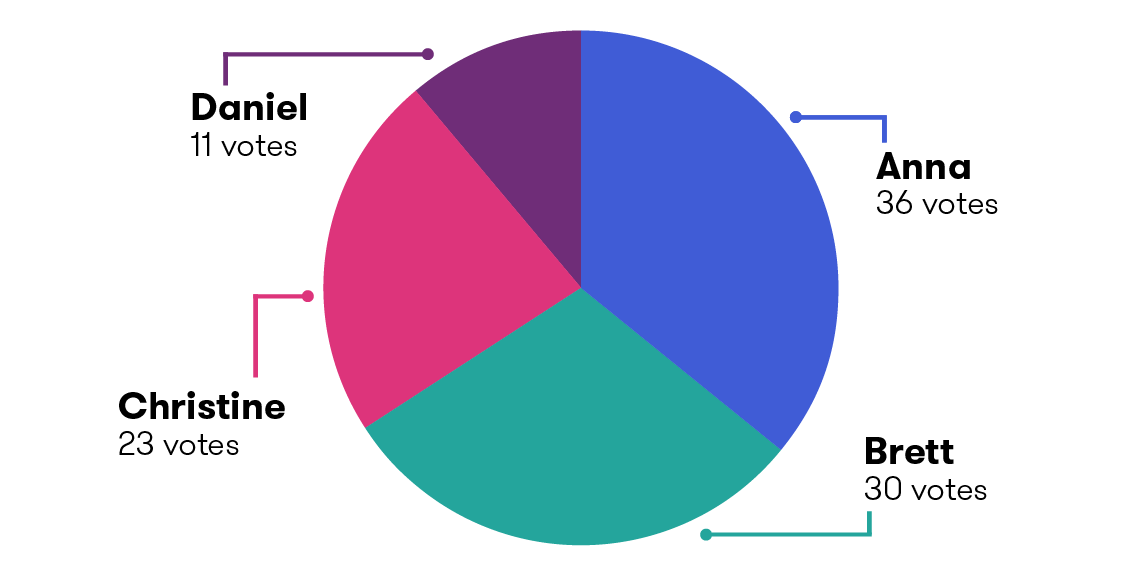
You can see that even though Anna got the most votes (36), there were almost twice as many people who didn’t vote for her (64).
An option used in some countries is to have several rounds of elections—the candidates with the least number of votes drop out, and the whole election is held again with fewer candidates, until someone gets more than half of all votes.
Rather than have several rounds of elections, which requires asking voters to vote more than once, it is mathematically possible to achieve the same result by asking voters to mark their preferences for all candidates. This is called a preferential system and it is used in Australia to elect our Parliament.
Preferential voting
In a preferential voting system you vote for each candidate in order of preference, rather than voting for just one candidate. This tells us every voter's first preference, second preference, third preference, and so on. After first votes are allocated, the candidate with the least number of votes drops out and their votes are given to the others according to preferences. This process is repeated until someone gets more than half the votes, as the following example shows.
Anna, Brett, Christine, and Daniel are again candidates in an election with 100 voters. The count starts with the first preferences, cast as follows.

| Candidate | First preference |
|---|---|
| Anna | 36 |
| Brett | 30 |
| Christine | 23 |
| Daniel | 11 |
| Total | 100 |
Daniel, with the least number of votes, drops out. His 11 votes are now given to their second preference: 3 votes had Anna at number 2, 6 had Brett at number 2, and 2 had Christine at number 2.
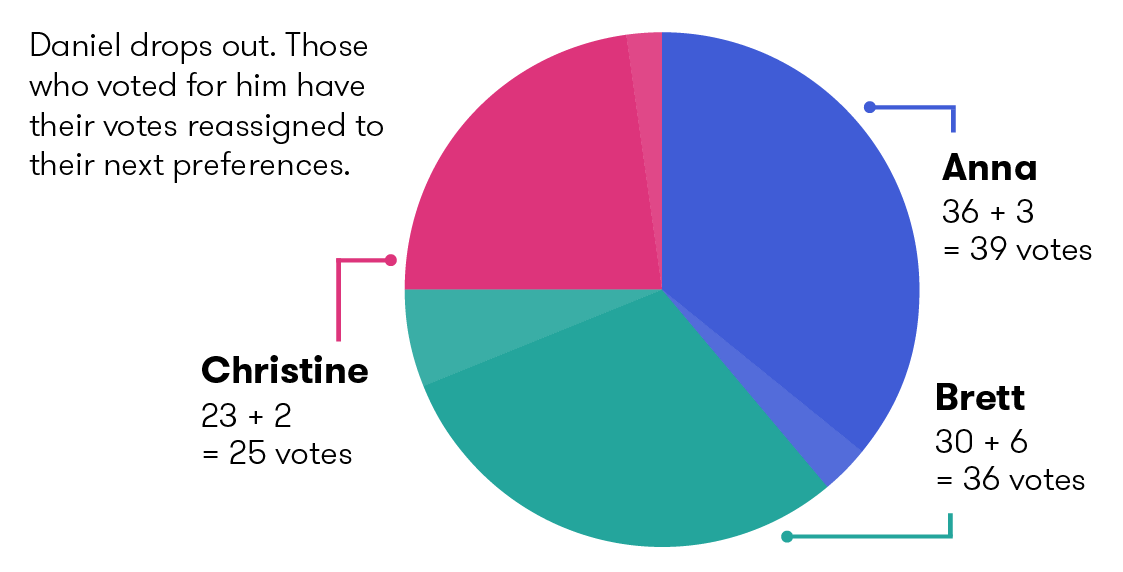
| Candidate | First preference | Reassigned votes: 1 Daniel | Total |
|---|---|---|---|
| Anna | 36 | 3 | 39 |
| Brett | 30 | 6 | 36 |
| Christine | 23 | 2 | 25 |
| Total | 89 | 11 | 100 |
Because no-one has more than half the number of votes, another candidate is dropped. This time Christine has the least number of votes so her votes are distributed according to their second preferences: 8 to Anna, 13 to Brett, and 2 to Daniel. But Daniel has already dropped out, so those last 2 go to the third preference, one each to Anna and Brett. The two votes that previously went from Daniel to Christine are now given to their third preference, this time both go to Brett. So now we have:
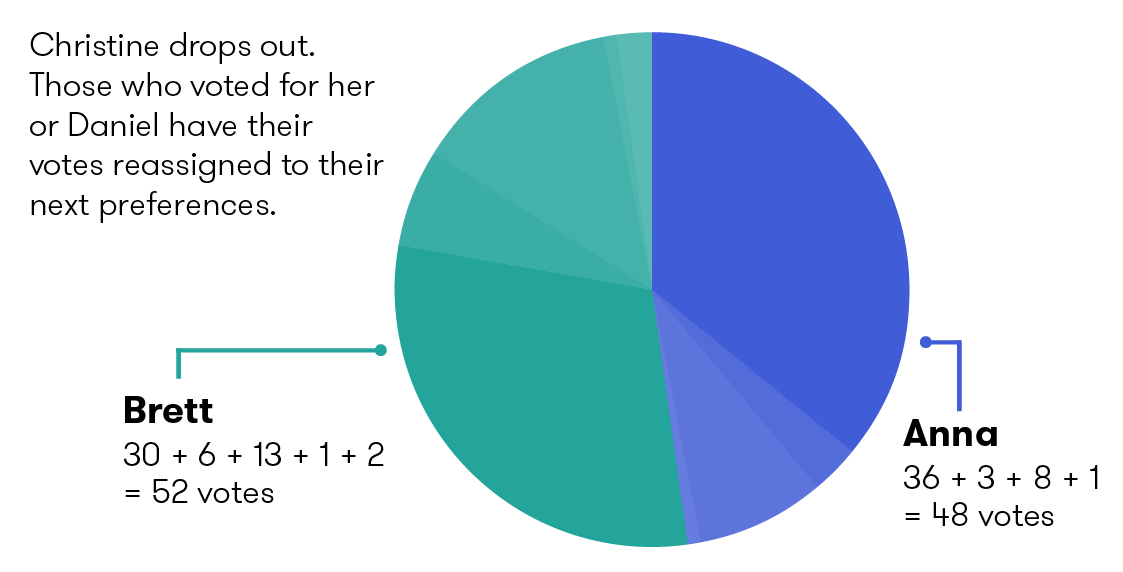
| Candidate | First preference | 1 Daniel |
1 Christine |
1 Christine2 Daniel |
1 Daniel2 Christine |
Total |
|---|---|---|---|---|---|---|
| Anna | 36 | 3 | 8 | 1 | 0 | 48 |
| Brett | 30 | 6 | 13 | 1 | 2 | 52 |
| Total | 66 | 9 | 21 | 2 | 2 | 100 |
Brett now has more than half the total vote so he gets elected.
Electing the Australian Parliament
The Australian Parliament has two chambers—the House of Representatives and the Senate.
The House of Representatives
Australia has 150 electorates that each elect a single member to the House of Representatives, using the preferential voting system.
Around 150,000 people live in the House of Representative electorates, with an average of 94,000 voters. Electorates have similar numbers of voters because each electorate gets exactly one vote in Parliament. It means that all Australians have roughly equal representation. But it does mean that more than half of all seats come from New South Wales and Victoria because more people live there.
New South Wales
representativesVictoria
representativesQueensland
representativesWestern Australia
representativesSouth Australia
representativesTasmania
representativesAustralian Capital Territory
representativesNorthern Territory
representativesThe Senate
There are only eight electorates for the Senate—the six States and two Territories. These electorates are much bigger than those for the House of Representatives but each State elects twelve Senators and each Territory elects two. Notice that New South Wales, with 5,126,651 voters, has as many senators as Tasmania with 375,024 voters—less than one-tenth as many as New South Wales (figures from September 2016).
New South Wales
representativesVictoria
representativesQueensland
representativesWestern Australia
representativesSouth Australia
representativesTasmania
representativesAustralian Capital Territory
representativesNorthern Territory
representativesOne of the reasons for creating the Senate was to give people in the less populated States more of a say in Parliament.
The Senate also uses preferential voting, but because more than one person is elected from each electorate the situation is more complex. Usually, a large number of candidates stand for Senate seats and for a voter, placing them all in order of preference can take a long time. For example, the ballot paper for the 2013 Senate election had so many candidates it was over one meter long and voters were handed magnifying glasses to help them read the document!

The ballot paper listing the Senate candidates for a particular state is divided by a horizontal line into two sections, and traditionally, voters had the option to vote ‘above the line’ or ‘below the line’. Single parties (the Labor Party, the Greens etc.) are listed above the line and a voter only had to select one box to tick. Below the line, all individual candidates are listed and, until the electoral changes of 2016, voters were required to allocate a preference to every candidate. Failure to do so rendered the vote invalid.
Obviously, not many voters choose the option of numbering all the boxes below the line to make their preferences clear, less than 5 per cent in fact. As a shortcut, the different political groups would work out their own preferences prior to the election. Known as ‘Group Voting Tickets’, they were a pre-assigned sequence of preferences—essentially, each party or group would negotiate with the other parties and candidates, making deals as to who got their preferences and how they were allocated. For example, if you voted above the line for the Australian Liberal Party, then your vote was distributed according to the wishes or preferences of that party.
Group Voting Tickets were criticised due to the fact that most voters had no way of knowing what deals their selected party had made or where their vote actually ended up. Although this information was available online, it was confusing and complex.
The situation came to a head at the 2013 election, when ‘preference whispering’ and backroom deals resulted in Motoring Enthusiast Party member Ricky Muir being elected with less than 0.51 per cent of the overall vote. His win was based solely on the distribution of preferences. His success, and that of several other ‘micro-party’ candidates elected via preferences, resulted in the decision being made that the system had to change.
Electoral reform for the Senate was introduced in 2016. These changes abolished Group Voting Tickets and instead replaced them with optional preferential voting. This means voters can now select multiple boxes above the line to assign their preferences for parties, or they can vote for individual candidates below the line, but now do not have to fill out every box, as they did previously (a welcome change considering there are often upwards of 70 boxes below the line). These changes are expected to result in fewer ‘informal’ (invalid) votes and should enable voters to have more of a say in where their vote ends up.
It was also decided that party logos would be included on the ballot paper to help voters distinguish between parties with similar-sounding names (such as the Liberal Party of Australia and the Liberal Democratic Party).
Another complication is that the State senators usually sit through two Parliaments – six Senate seats are filled at one election and the other half at the next election. (There are rare situations when all twelve Senate seats are up for election.) The Territories elect two Senators at each election.
The number of votes needed to win a Senate seat is called a quota GLOSSARY quotaThe number of votes needed to win a Senate seat. The value of the quota is determined by how many senators are being elected. .
- the quota needed when there are two senators being elected is one vote more than one-third of all votes.
- the quota needed when there are six senators being elected is one vote more than one-seventh of all votes.
- the quota needed when there are twelve senators being elected is one vote more than one-thirteenth of all votes.
Counting the Senate vote
Let’s have a look at how votes and preferences are allocated. Emiko, Gerard, Harry and Ingrid are candidates for two Senate seats in the Australian Capital Territory, in an election where there were 200,987 formal votes. First, the quota that a candidate requires to be elected is calculated.
quota=(200,987÷3)+1=66,996
So, a candidate needs to get 66,996 votes to be elected.
The first step in counting is the allocation of the first preferences.
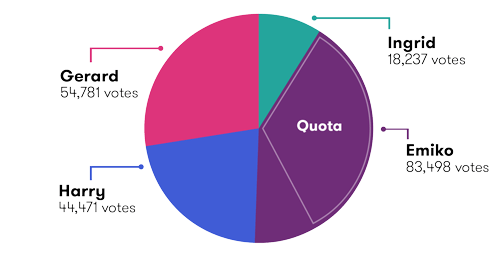
| Candidate | First preference |
|---|---|
| Ingrid | 18,237 |
| Emiko | 83,498 (quota reached) |
| Harry | 44,471 |
| Gerard | 54,781 |
Emiko has reached the quota and is elected.
Emiko received 16,502 votes more than the required quota of 66,996; these are surplus votes GLOSSARY surplus votesThe remaining votes a candidate receives beyond the quota. . Her surplus votes will now be transferred to the voters' next preferred candidate. However, the voters that voted for Emiko as their first preference will not always list the same candidate as their second preference, and we have to take this into account when we allocate Emiko’s surplus votes. The process will be to transfer all her votes, but at a reduced value, known as the transfer value GLOSSARY transfer valueThe value that transferred surplus votes are multiplied by, to reduce the value of those votes. The transfer value is the number of surplus votes from the person whose votes are being transferred, divided by the total number of that person's votes. .
The transfer value is calculated as a decimal proportion of the candidate's total vote:
transfer value=number of surplus votes÷total number of votes
Emiko’s transfer value is:
16,502÷83,498=0.19763347
The result is calculated to eight decimal places, with no rounding.
All of Emiko’s 83,498 votes are then transferred to the voter's second preference, and multiplied by the transfer value of 0.19763347.
55,009 of Emiko’s second preferences go to Ingrid.
55,009×0.19763347=10,871 votes
After the transfer value is applied, Ingrid gets 10,871 extra votes. The exact result of this calculation was 10,871.61, but only full votes can be transferred, so this figure is rounded down to the nearest whole number.
Harry gets 24,977 of Emiko’s second preferences.
24,977÷0.19763347=4,936 votes
Gerard gets 3,512 of Emiko’s second preferences.
3,512÷0.19763347=694 votes
So, now we have:
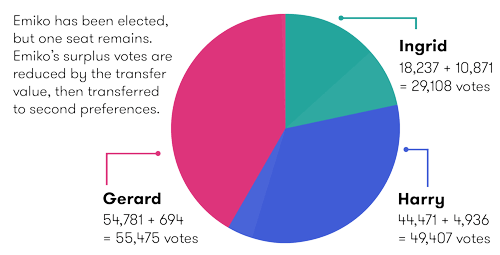
| Candidate | First preference | Transfer votes from Emiko's surplus | Total |
|---|---|---|---|
| Gerard | 54,781 | 694 | 55,475 |
| Harry | 44,471 | 4,936 | 49,407 |
| Ingrid | 18,237 | 10,871 | 29,108 |
The number of transfer votes allocated after application of the transfer value matches Emiko’s surplus:
694+4,396+10,871=16,501
Application of the transfer value divides all of Emiko's first preference votes into the portion required for her to reach the quota, and the portion that is available to be transferred to the next preferred candidate.
At this stage, none of the three remaining candidates have reached the quota of 66,996 votes. And even though Ingrid received most of Emiko's surplus, at this point she will be excluded because she has the least number of votes.
Ingrid’s 18,237 first preference votes are now distributed as follows:
- Votes with Gerard or Harry as second preference go straight to them.
- Votes with Emiko as second preference go to the voter's third preference, which must be either Gerard or Harry.
Gerard receives 1,223 of these preference votes and Harry 17,014 (the people that voted for Ingrid were much less likely to preference Gerard!).
This situation now is:
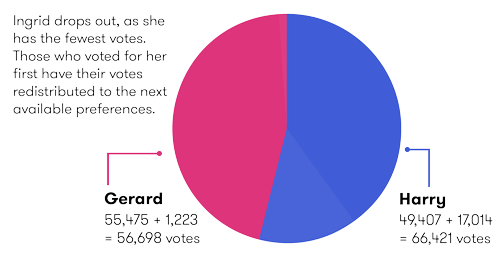
| Candidate | Votes after transfer of Emiko's surplus | Ingrid's votes, redistributed by second preference | Total |
|---|---|---|---|
| Gerard | 55,475 | 1,223 | 56,698 |
| Harry | 49,407 | 17,014 | 66,421 |
Now we need to consider the 55,009 transfer votes that Ingrid received from Emiko's surplus. These votes are transferred to either Gerard or Harry, whichever candidate is given the highest preference. They are transferred at the same reduced transfer value at which Ingrid received them.
Of Emiko's surplus votes received by Ingrid, 16,879 of them preferenced Gerard, so he gets:
16,897×0.19763347=3,335 extra votes
Harry was preferenced in 38,130 of these votes, so he gets:
38,130×0.19763347=7,535 extra votes
Again, the total number of votes transferred matches the reduced value of the votes received by Ingrid from Emiko's surplus:
3,335+7,535=10,870
The final picture is:
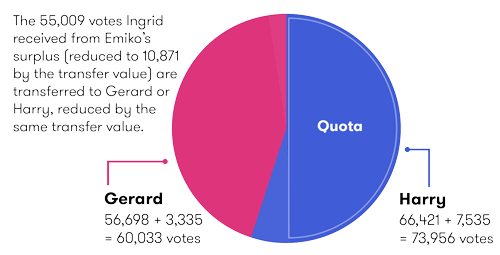
| Candidate | Votes after transfer of Emiko's surplus and Ingrid's exclusion | Transfer votes from Ingrid's share of Emiko's surplus | Total |
|---|---|---|---|
| Gerard | 56,698 | 3,335 | 60,033 |
| Harry | 66,421 | 7,535 | 73,956 (quota reached) |
Harry reaches the quota and is elected to the second seat. Congratulations Harry!